반응형
모델이 있고, 그 모델을 입력값에 원하는 출력을 맞추는 작업이다.
모델을 이루는 파라미터들(Weight 값 등)을 찾는 과정을 MLE라고 한다.
Systematic Approach
체계적인 접근. 확률에 근거하여 나오는 이론.
Likelihood vs Probability
Probability(확률)
가방이 있고, 공이 두개(0, 1)가 있다.
가방안에 손을 집어넣고 꺼낸후 다시 집어넣는다.

확률 p(x) : x가 발견될 확률이다.
Likelihood
이산수학적으로 나뉘어 있다면 확률과 Likelihood는 동일하다.
하지만 연속된 값에서는 다른 의미를 가진다.

위 그래프에서의 확률은 그래프 아래의 값(색칠된 값)이 되고, Likelihood는 Y축의 값이 된다.
특정한 x값에 대한 y의 값이다.
머신러닝에서는 최대의 likelihood값이 가장 좋은 결과값을 나타낼 것이다.
Normal Distribution Model
1차원 데이터




x : x축의 값 u : 평균값 o : 표준편차 (u와 o를 합쳐 세타로 표현한다.)
값이 크면 뾰족한 그래프가 된다.
x에 따른 likelihood가 바뀌는 모델이 된다.
Data중 1개
평균과 표준편차 값을 바꾸고 있다.
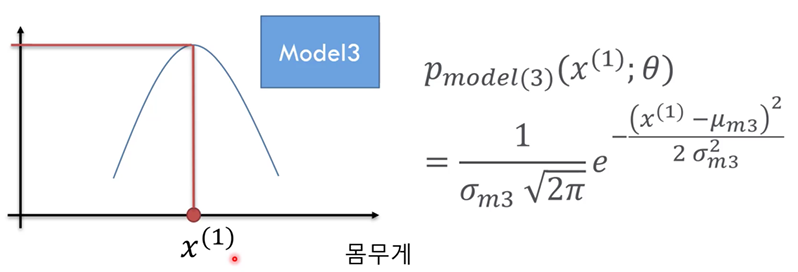
위와같은 과정의 반복을 통해 likelihood가 Maximize 한 모델을 찾는다.
해당 수식은 아래와 같다.

pθ(x;θ) = likelihood
Data중 2개

x1과 x2는 x축 위의 점이다.
서로 독립적이고 identical하다.
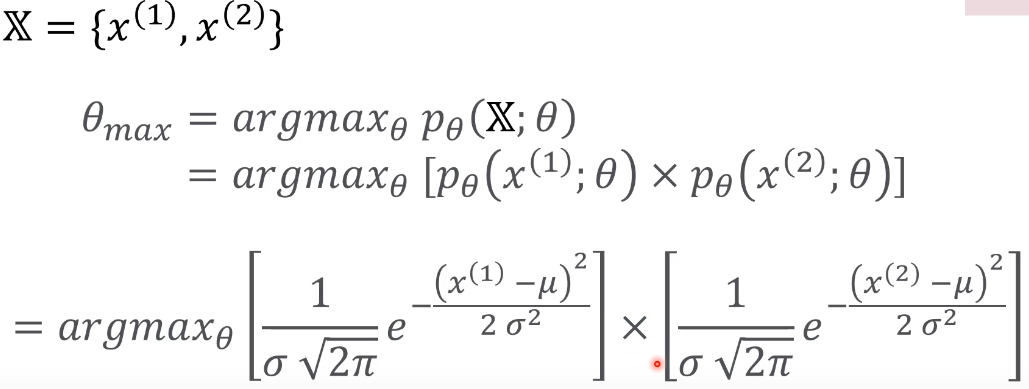
Data가 m개 모델
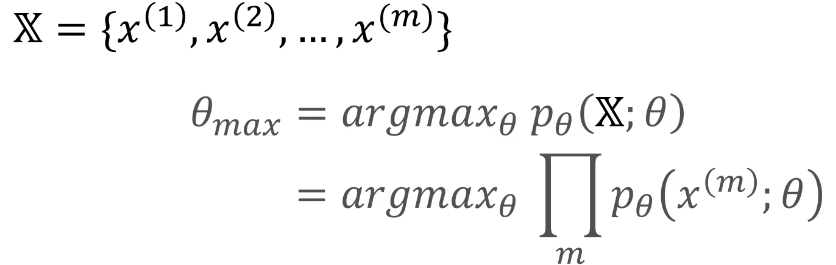
위 수식은 곱하기로 구성되어 있기에 결과의 변동의 폭이 매우 크다.
위 수식의 목적은 likelihood가 최대값이 되는것을 원하기 때문에 아래의 식으로 변경한다

이를 통해 곱하기는 덧셈으로 바꾸어 사용할 수 있다.
반응형
'머신러닝' 카테고리의 다른 글
| Bayesian Estimation (0) | 2021.05.26 |
|---|---|
| Maximum likelihood Estimation 2 (0) | 2021.05.16 |
| 머신러닝이란? (0) | 2021.05.14 |
| Batch Normalization 2 & Well - Known Models & Recurrent Neural Network (0) | 2021.04.28 |
| Batch Normalization & Overfitting & HyperParameter (0) | 2021.04.23 |




댓글