현재의 구조
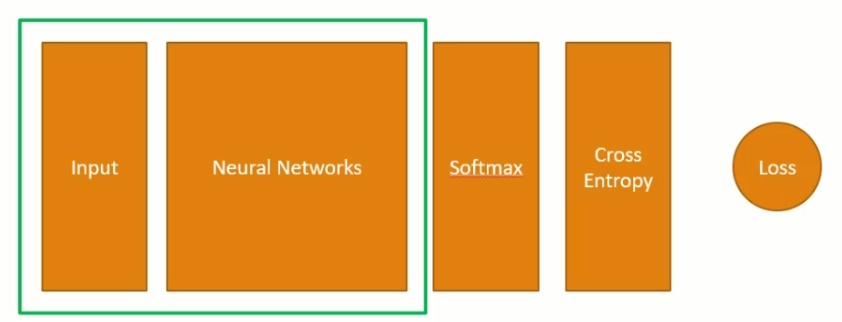
Input과 NN

- Bias는 Hidden Layer와 Output Layer(들어가지 않는 경우도 존재)에만 들어간다. (Input Layer은 사용하지 않는다.)
- Weight 값은 Input -> Hidden Layer 에서 6개, Hidden -> Output Layer에서 9개 존재하고 있다.
- 활성함수는 Hidden Layer에 보통 사용한다. 따라서 Output Layer에는 음수가 출력될 수 있다.
Softmax와 Cross Entropy의 적용과정

- 인풋이 1개라면 Loss는 1개, 2개라면 2개이다.
- Loss는 인풋에 따라 결정된다.
- Loss는 Input 부터 순차적으로 값이 결정되는데 이를 Feed-Forward라고 지칭한다.
- 이 과정에서 Weight, Biases 값은 변하지 않는다.
- Loss는 input의 결과값이 레이블과 얼마나 떨어져 있는가 > 로스값을 줄여야함.
- 학습 : 로스값을 최소화 할 수 있는 W, B 값을 구하는것.
Back - Propagation의 착안점
- x 가 0.1 0.01 0.001 변할때 f(x)는 얼마나 변하는가?
-> 극한으로 이것을 보낸다면, 아래와 같아진다.

Back - Propagation에서의 필요한 공식
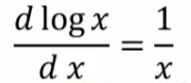

Back- Propagation
- 위와 같은 과정을 거꾸로 추적할 수 있고 이를 역전파라고 지칭함.
- w값과 b값의 변화에 따른 Loss의 변화량

- w값이 증가할 때 Loss가 증가한다면 w를 줄이면 됨.
- w값이 증가할 때 Loss가 증가한다면 w를 증가시키면 됨.
이는 아래와 같은 과정을 거친다

이것을 반영하여서, 새로운 w 값은 아래와 같다.

1번 dloss / dsoft


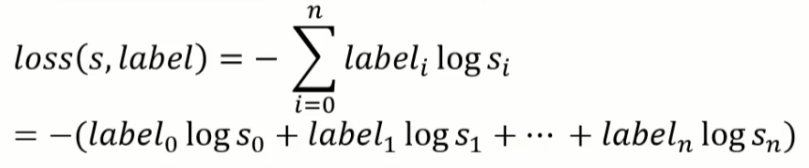
이는 다음과 같다.


이어서 dl / ds0를 보자.

s1 = 1-s0+...+sn 이기에 s1을 s0로 미분한다면 -1이 된다. 따라서
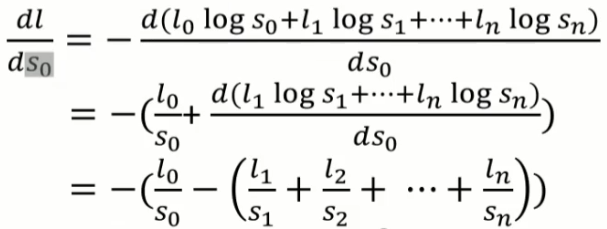
이를 시그마를 이용해서 표현한다면,

예를들어 만약 n = 1인 경우에는 아래와 같이 두가지의 값이 나온다.

여기까지 dl / dsoft 까지의 과정이다.
다음글
Back - Propagation 2
2. dsoft / do 이 경우를 2차원으로 그림으로 표현하자면, 따라서 dl/dO0 는 3. do/dw - 두번째 w값에 대한 Loss의 변화량을 구하기 위함 앞서 Output Layer에서는 ReLU를 적용시키지 않는다 하였기 때문에,..
5sangs.tistory.com
'머신러닝' 카테고리의 다른 글
| Back - Propagation 3 (0) | 2021.06.18 |
|---|---|
| Back - Propagation 2 (0) | 2021.06.18 |
| 인공신경망의 학습 (0) | 2021.06.17 |
| 인공신경망의 기초 (0) | 2021.06.17 |
| 여러가지 모델 (1) | 2021.06.08 |



댓글