기존 RNN의 문제점
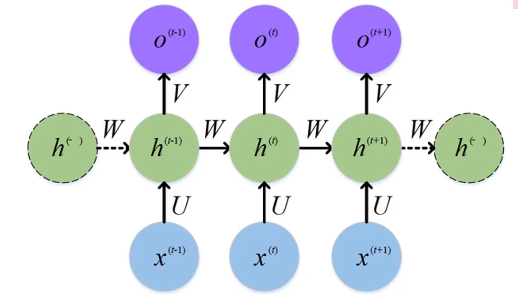
기존의 RNN은 초기 입력값의 영향이 점점 사라진다.
-> Back propagation을 통한 여러 번의 미분이 이유이다. (장기기억된 것은 Weight 값이 낮아진다.)
Long Short - Term Memory
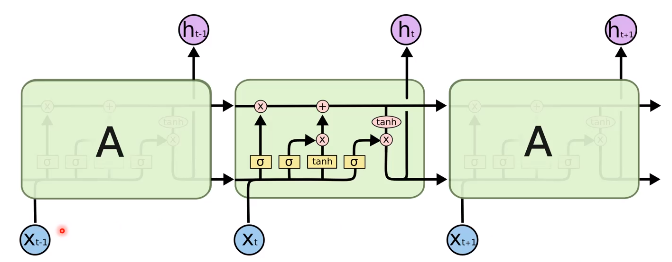
RNN의 확장모델인 LSTM을 보자.
Cell State

Cell State는 Matrix / Vector 구조를 가진다.
RNN & LSTM은 Sigmoid Activate Function을 이용한다.
X : Pointwise 곱셈. 요소별로 곱해줌.
+ : Pointwise 덧셈. 요소별로 더해줌


위 식에대한 연산은 다음과 같다.
망각 게이트 (Forget Gate)

1. Concat 연산
Concat 연산의 식은 아래와 같다.


위 식의 입력값에 대한 Concat 연산은 아래의 값과 같다.

2. 가중치 Wf와 Bias bf.

위의 식은 시그모이드 활성 함수를 통해 약 -5 이하의 값은 0으로 5 이상의 값은 1이 된다.

3. Cell State의 입력값과 시그모이드값의 곱
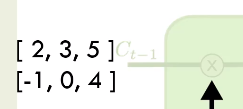
해당 값은 [2, 0, 5] [-1, 0, 4]로 변한다.
입력 게이트 (Input Gate)
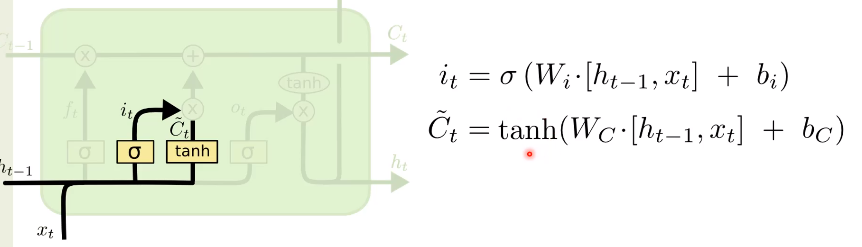
it : 망각 게이트와 식이 같고, W의 값이 다름.
~Ct : tanh 를 통해 새로운 정보를 선택적으로 전송.
it의 계산

~Ct의 계산

it x ~Ct의 계산

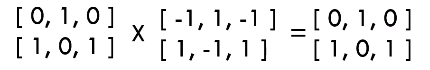
새로운 Ct의 계산

출력게이트 (Output Gate)

Torch.nn.LSTM

- 기본적으로 위의 두 식은 같은 역할을 한다
- 오른쪽 식은 벡터가 같은 형태여야만 연산이 가능하다.
정리
LSTM이란 RNN을 확장시켜서 만든 것.
뒤로 갈수록 비중이 줄어드는 장기기억을 Cell State를 통하여 연결하여 뉴럴 넷의 구조를 만드는 것.
뉴럴렛을 학습시킨다 : 원하는 가중치값을 찾기 위해 출력 값과, 레이블과의 거리를 CE/MSE 등을 사용하여 Loss Function을 정의하고 그 거리를 줄이기 위한 가중치값들을 찾는 것.
LSTM에서는 Wf, Wi, Wc, Wo와 bf, bi, bc, bo가 찾아야 하는 가중치의 값이다.
LSTM은 단순한 RNN보다 장기 기억에서 필요한 정보를 저장할 수 있다는 장점이 있다.
'머신러닝' 카테고리의 다른 글
| 인공신경망의 기초 (0) | 2021.06.17 |
|---|---|
| 여러가지 모델 (1) | 2021.06.08 |
| Maximum A Posteriori Estimation (0) | 2021.05.27 |
| Bayesian Estimation (0) | 2021.05.26 |
| Maximum likelihood Estimation 2 (0) | 2021.05.16 |




댓글